How to Derive the Equation of a Circle from the Endpoints of Its Diameter
To find the equation of a circle given the endpoints A and B of its diameter, follow these steps:
- Find the center of the circle
The center \( C \) of the circle is the midpoint of the line segment connecting points \( A \) and \( B \) (the endpoints of the diameter). If \( A \) has coordinates \((x_A, y_A)\) and \( B \) has coordinates \((x_B, y_B)\), the center \( C \) will have coordinates: $$ \left( \frac{x_A + x_B}{2}, \frac{y_A + y_B}{2} \right) $$ - Calculate the radius
The radius \( r \) is half the distance between points \( A \) and \( B \). The distance between \( A \) and \( B \) can be found using the Euclidean distance formula: $$ AB = \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$ So, the radius \( r \) is: $$ r = \frac{1}{2} \cdot \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$ - Write the equation of the circle
Once the center \( C(x_0, y_0) \) and the radius \( r \) are known, the equation of the circle can be written in standard form: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$ where \( x_0 = \frac{x_A + x_B}{2} \) and \( y_0 = \frac{y_A + y_B}{2} \).
A Practical Example
Let's go through a practical example to make the process clear.
Consider two points \( A(2, 3) \) and \( B(8, 7) \) which are the endpoints of a diameter of a circle.
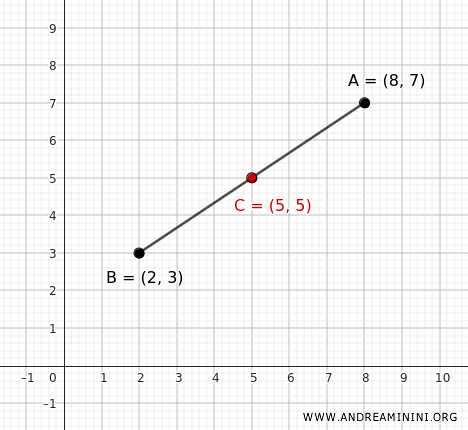
The center \( C \) is the midpoint of the segment \( AB \):
$$ C \left( \frac{x_A + x_B}{2}, \frac{y_A + y_B}{2} \right) $$
$$ C \left( \frac{2 + 8}{2}, \frac{3 + 7}{2} \right) $$
$$ C \left( \frac{10}{2}, \frac{10}{2} \right) $$
$$ C(5, 5) $$
Therefore, the center of the circle is at coordinates \( C(5, 5) \) on the Cartesian plane.
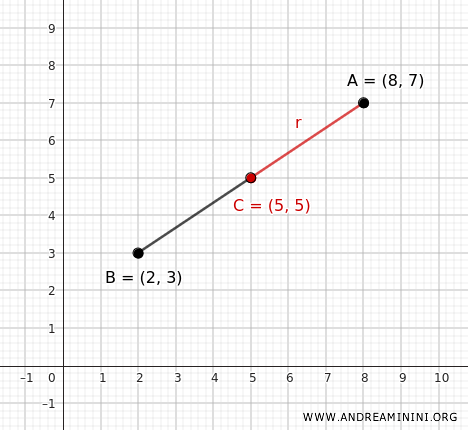
The distance \( AB \) between points \( A \) and \( B \) is calculated using the Euclidean distance formula:
$$ AB = \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$
$$ AB = \sqrt{(2 - 8)^2 + (3 - 7)^2} $$
$$ AB = \sqrt{(-6)^2 + (-4)^2} $$
$$ AB = \sqrt{36 + 16} $$
$$ AB = \sqrt{52} $$
$$ AB = 2\sqrt{13} $$
Since the radius of the circle is half the diameter, we divide the distance \( AB \) by two:
$$ r = \frac{1}{2} \cdot AB $$
$$ r = \frac{1}{2} \cdot 2\sqrt{13} $$
$$ r= \sqrt{13} $$
Therefore, the radius is \( r= \sqrt{13} \).
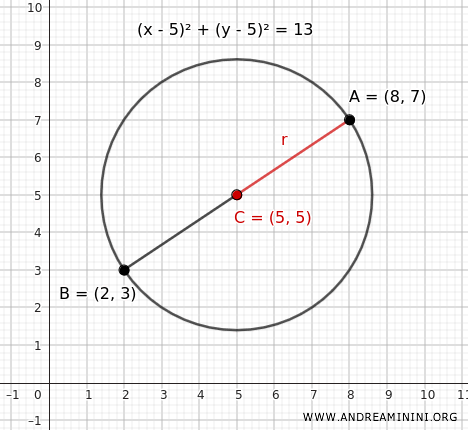
Now we can write the equation of the circle with center \( C(5, 5) \) and radius \( r = \sqrt{13} \).
The formula for the circle given the center and radius is as follows:
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
In this case, the coordinates of the center are \( x_0 = 5 \) and \( y_0 = 5 \), so the equation becomes:
$$ (x - 5)^2 + (y - 5)^2 = (\sqrt{13})^2 $$
$$ (x - 5)^2 + (y - 5)^2 = 13 $$
This is the equation of the circle with a diameter whose endpoints are \( A(2, 3) \) and \( B(8, 7) \).
And that's how it's done.
