Methematics and Computer Science
Set Theory
Set theory is a fundamental branch of mathematics focused on the study of sets, which are collections of well-defined and distinct objects. The objects that comprise a set are known as elements or members. A set is viewed as a single entity that encompasses its elements. Sets are typically denoted by uppercase letters (A, B, C, ...), while their elements are listed within curly braces. For instance, the set A containing the numbers 1, 2, and 3 is written as: A={1,2,3}.
Matrix
A matrix is an organized set of numbers arranged in rows and columns, represented as a rectangular array where each number is referred to as an element of the matrix. Typically, a matrix is denoted by an uppercase letter, such as \( A \), and its elements are indicated by a lowercase letter with two indices, such as \( a_{ij} \), where \( i \) represents the row and \( j \) the column. Matrices were introduced in the 17th century by the English mathematician James Joseph Sylvester. However, it was Arthur Cayley in the 19th century who advanced the modern theory of matrices.
Vectors
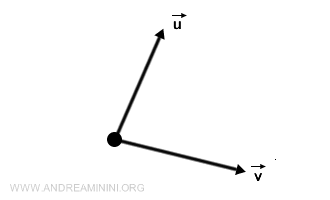A vector is a mathematical quantity that possesses both magnitude and direction, represented by an arrow in geometric space. In notation, a vector is often indicated by a lowercase bold letter, such as $ \vec{v} $, or with an arrow above the letter, like \(\vec{v}\). Vectors can be described through their components, which represent the projections along the axes of a coordinate system. For example, a two-dimensional vector $ \vec{v} $ can be represented as \((v_x, v_y)\), where \(v_x\) and \(v_y\) are the components along the x and y axes, respectively. The theory of vectors has ancient roots, but it was the French mathematician Augustin-Louis Cauchy in the 19th century who formally developed the concept and its use in physical sciences and engineering.
