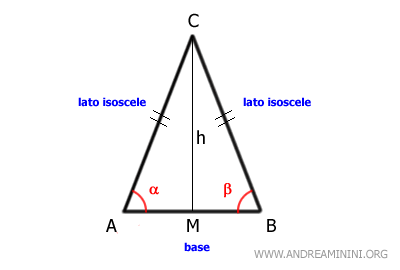
Angle Bisector in an Isosceles Triangle

In an isosceles triangle, the bisector of the vertex angle opposite the base also serves as the median and the altitude.

The Proof

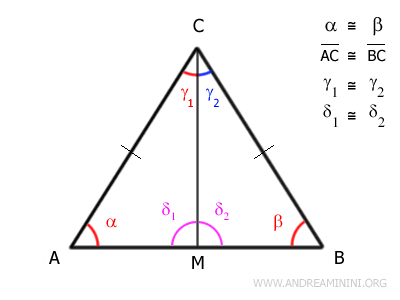
Let’s take an isosceles triangle ABC.

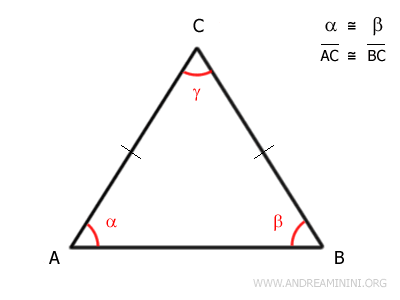
Since triangle ABC is isosceles, sides AC and BC are congruent, and the angles adjacent to the base - α and β - are also congruent.

$$ \overline{AC} = \overline{BC} $$

$$ \alpha = \beta $$

Now draw the angle bisector CM from the vertex angle γ to the base AB.

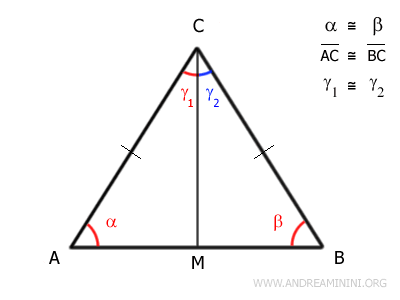
The bisector CM divides the vertex angle γ into two equal parts:

$$ \gamma_1 \cong \gamma_2 $$

This construction splits the triangle into two smaller triangles, ACM and BCM, which have:

• a common side CM
• two congruent sides: AC ≅ BC
• congruent included angles: γ₁ ≅ γ₂

By the Side-Angle-Side congruence criterion, the triangles AMC and BMC are congruent:

$$ AMC \cong BMC $$

Because these triangles are congruent, all their corresponding sides and angles are equal. In particular, segments AM and BM are congruent:

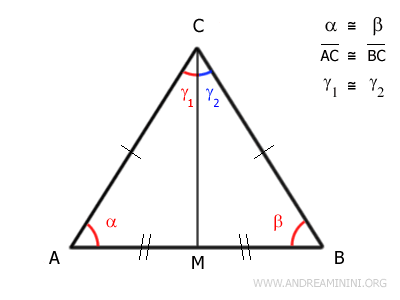
$$ AM \cong BM $$

This means that M is the midpoint of AB. So, the bisector CM also acts as the median to the base of the triangle.

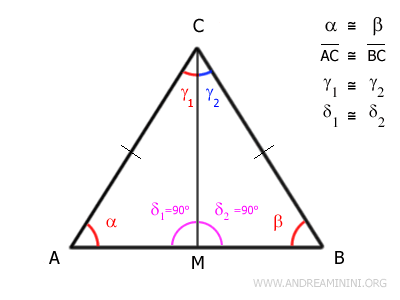
Since AMC and BMC are congruent, all corresponding angles are equal. In particular, angles δ₁ and δ₂ are congruent:

$$ \delta_1 \cong \delta_2 $$

These two angles are also supplementary, meaning:

$$ \delta_1 + \delta_2 = 180^\circ $$

When two congruent angles are also supplementary, each must measure 90°:

$$ \delta_1 = \delta_2 = 90^\circ $$

This confirms that the bisector CM is also the altitude of the isosceles triangle.

And so on.