Extended Pythagorean Theorem
For any right-angled triangle, if you construct three similar polygons on its sides, the area of the polygon on the hypotenuse equals the sum of the areas of the polygons on the two legs.
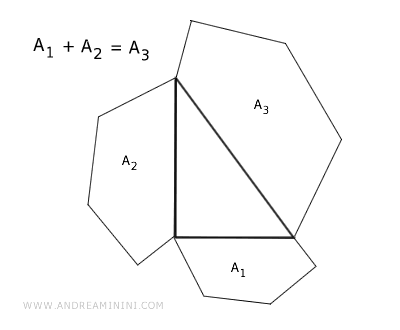
Put simply, the area of the polygon on the hypotenuse mirrors the combined areas of the polygons on the legs.
This theorem broadens the concept, showing that the relationship described by Pythagoras' theorem isn't confined to squares but extends to any similar geometric shapes built on those sides.
Note: This implies that whether triangles, circles, regular polygons, or any other analogous shape are constructed on the triangle's three sides, the total area of the shapes on the legs will always match the area of the shape on the hypotenuse.
An Illustrative Example
Take a right triangle ABC, for instance, where I've constructed three regular pentagons on its sides.
The legs of the triangle, AB and AC, measure 4 and 3 units, respectively, while the hypotenuse BC spans 5 units.
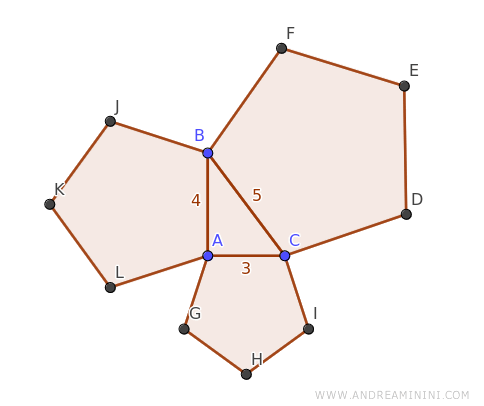
Since the pentagons are regular polygons with an equal number of sides, they qualify as similar polygons.
Note: The theorem does not stipulate that the polygons must be regular. They can be irregular as long as they maintain similarity. In this case, regular polygons were chosen for simplicity in calculating areas. Plus, regular polygons with an equal number of sides are invariably similar.
Let's calculate the areas of these pentagons.
The area of a regular polygon is calculated as the semiperimeter (p) times the apotem (a).
$$ A = p \cdot a $$
For a pentagon, the apotem (a) is the product of a side (l) and a constant (f), which is 0.688 for pentagons.
$$ A = p \cdot ( l \cdot f ) $$
$$ A = p \cdot ( l \cdot 0.688 ) $$
The area of the pentagon on leg AB (length 3) is A1=15.48 square units.
$$ A_1 = \frac{3 \cdot 5}{2} \cdot ( 3 \cdot 0.688 ) = 15.48 $$
The area of the pentagon on leg AC (length 4) is A2=27.52 square units.
$$ A_2 = \frac{4 \cdot 5}{2} \cdot ( 4 \cdot 0.688 ) = 27.52 $$
The area of the pentagon on the hypotenuse BC (length 5) is A3=43 square units.
$$ A_3 = \frac{5 \cdot 5}{2} \cdot ( 5 \cdot 0.688 ) = 43 $$
A quick check with Geogebra confirms the accuracy of these areas:
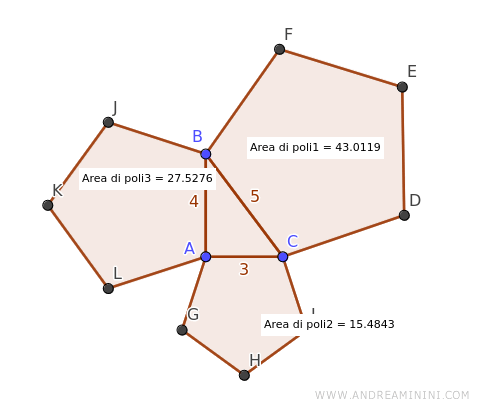
Ensuring the sum of the areas on the legs equals the area on the hypotenuse:
$$ A_1 + A_2 = A_3 $$
With A1=15.48 and A2=27.52:
$$ 15.48 + 27.52 = 43 $$
$$ 43 = 43 $$
Indeed, the combined area of the polygons on the legs is equal to the area of the polygon on the hypotenuse.
The Proof
Consider the same setup of a right-angled triangle with three similar polygons on its sides.
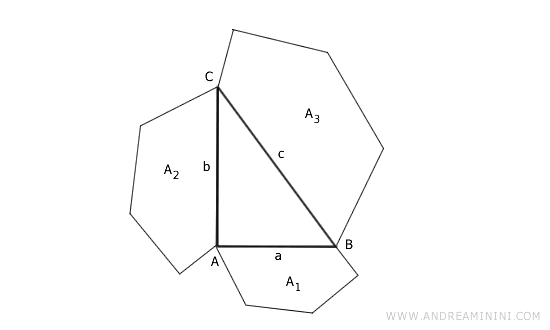
According to the theorem on the areas of similar polygons, their areas relate to the square of the sides they're built on.
$$ \frac{A_3}{A_2} = ( \frac{c}{b} )^2 $$
Hence,
$$ A_3 = A_2 \cdot ( \frac{c}{b} )^2 $$
$$ A_3 = A_2 \cdot \frac{c^2}{b^2} $$
Given that similar polygons have sides in proportional ratio k:
$$ k = \frac{a}{b} $$
And by Pythagoras' theorem, the sum of squares on the legs equals the square on the hypotenuse:
$$ c^2 = a^2 + b^2 $$
With k as a/b, a=kb, thus:
$$ c^2 = (kb)^2 + b^2 $$
$$ c^2 = k^2 b^2 + b^2 $$
$$ c^2 = b^2 (k^2 + 1) $$
So, returning to the ratio of the areas of similar polygons, we can replace c2 with b2(k2+1)
$$ A_3 = A_2 \cdot \frac{c^2}{b^2} $$
$$ A_3 = A_2 \cdot \frac{b^2 (k^2 + 1)}{b^2} $$
$$ A_3 = A_2 \cdot (k^2 + 1) $$
To prove that A1+A2=A3, I must demonstrate that A1+A2=A2(k2+1)
Knowing that k=a/b, according to the theorem of areas of similar polygons, we deduce that k2 is the ratio between the areas of similar polygons constructed on the legs a and b.
$$ k^2 = \frac{A_1}{A_2} $$
That is
$$ A_1 = k^2 \cdot A_2 $$
Knowing that A1=k2A2, I can rewrite the sum A1+A2 as follows
$$ A_1 + A_2 = ( k^2 \cdot A_2 ) + A_2 $$
$$ A_1 + A_2 = A_2 \cdot (k^2 +1 ) $$
This proves that A1+A2=A3 since A1+A2=A2(k2+1) and A3=A2(k2+1)
$$ A_1 + A_2 = A_2 \cdot (k^2 +1 ) = A_3 $$
Therefore, the sum of the areas of the similar polygons constructed on the legs is equal to the area of the polygon constructed on the hypotenuse.
Alternate Proof
Starting again with our right triangle ABC and the three similar polygons on its sides:

The initial hypothesis assumes similarity among these polygons.
Thus, according to the theorem of areas of similar polygons, the ratio of their areas equals the square of the ratio of corresponding sides:
$$ \frac{A_1}{A_2} = ( \frac{a}{b} )^2 $$
$$ \frac{A_1}{A_2} = \frac{a^2}{b^2} $$
Meaning, the area ratio of polygons on the legs mirrors the ratio of squares on those legs.
Marking the squares as Q1=a2 and Q2=b2:
$$ \frac{A_1}{A_2} = \frac{Q_1}{Q_2} $$
This logic also applies to the hypotenuse:
$$ \frac{A_3}{A_2} = \frac{Q_3}{Q_2} $$
Focusing on the first proportion
$$ \frac{A_1}{A_2} = \frac{Q_1}{Q_2} $$
Applying the property of composing proportions
$$ \frac{A_1+A_2}{A_2} = \frac{Q_1+Q_2}{Q_2} $$
According to Pythagoras' theorem, the sum of the squares on the legs Q1+Q2=Q3 equals the square on the hypotenuse.
$$ \frac{A_1+A_2}{A_2} = \frac{Q_3}{Q_2} $$
Knowing that A3/A2=Q3/Q2
$$ \frac{A_1+A_2}{A_2} = \frac{A_3}{A_2} $$
Simplifying yields
$$ A_1 + A_2 = A_3 $$
This demonstrates that the sum of the areas of the similar polygons constructed on the legs of the right triangle is equal to the area of the similar polygon constructed on the hypotenuse.
