Law of Conservation of Momentum

The law of conservation of momentum states that in an isolated system (one with no external forces), the total momentum $ \vec{P} $ remains constant: $$ \vec{P} = \sum_i m_i \vec{v}_i $$ where $m$ is the mass of each particle and $\vec{v}$ its velocity.

Momentum combines both mass and velocity:

$$ \vec{p} = m \vec{v} $$

This quantity measures the influence of a moving body when it interacts with others, since it depends on both speed and mass.

For example, a truck has a large mass, so even moving slowly it carries significant momentum. A ping-pong ball, by contrast, is so light that even at high speed its momentum is negligible.

According to the law of conservation of momentum, if no external force acts on a system, the total momentum before and after any interaction remains unchanged:

$$ \vec{P}_{\text{initial}} = \vec{P}_{\text{final}} $$

Momentum is therefore a conserved quantity, but only in a closed, isolated system.

A Simple Example

Imagine two skaters on perfectly smooth ice.

At first they are both at rest, so the total momentum is zero. When they push off one another, one glides to the right and the other to the left.

The momentum of one skater is equal and opposite to that of the other, so the total remains zero, just as it was initially.

In other words, if the net external force is zero ($\vec{F}_{\text{ext}}=0$), then:

$$ \frac{d\vec{P}}{dt} = 0 \quad \Rightarrow \quad \vec{P}_{\text{initial}} = \vec{P}_{\text{final}} $$

Example 2

Consider two billiard balls, each with a mass of 200 grams, moving with different initial velocities:

• Ball A: $m_A = 0.2 \,\text{kg}$, initial velocity $v_A = 5 \,\text{m/s}$.
• Ball B: $m_B = 0.2 \,\text{kg}$, initially at rest ($v_B = 0$).

Ball A moves at 5 m/s while Ball B is stationary.

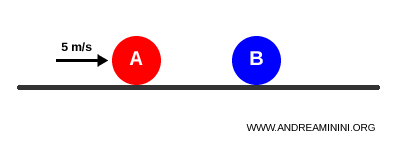
Before the collision, the system’s total momentum is 1 kg·m/s:

$$ p_{\text{tot}} = m_A v_A + m_B v_B = 0.2 \cdot 5 + 0.2 \cdot 0 = 1.0 \,\text{kg·m/s} $$

When Ball A collides head-on with Ball B:

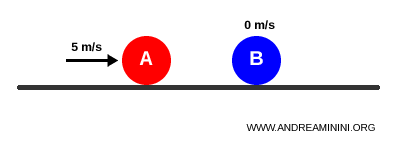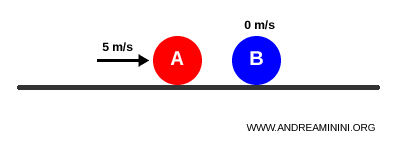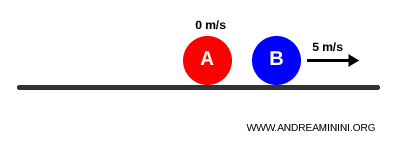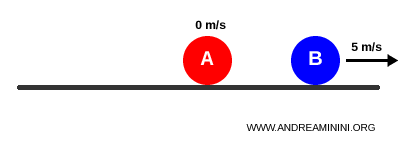
After the elastic collision, Ball A comes to rest while Ball B moves at 5 m/s:

$$ v_A' = 0 \qquad v_B' = 5 \,\text{m/s} $$

Total momentum remains unchanged:

$$ p_{\text{tot, final}} = m_A v_A' + m_B v_B' = 0.2 \cdot 0 + 0.2 \cdot 5 = 1.0 $$

Thus, in both elastic and inelastic collisions, the total momentum of the system is conserved.

Example 3

Consider a rifle of mass $m_f = 4 \,\text{kg}$ and a bullet of mass $m_p = 0.02 \,\text{kg}$.

Initially the rifle is at rest, so the total momentum is zero:

$$ p_{\text{initial}} = 0 $$

When the rifle fires, the bullet leaves the barrel at $v_p = 400 \,\text{m/s}$.

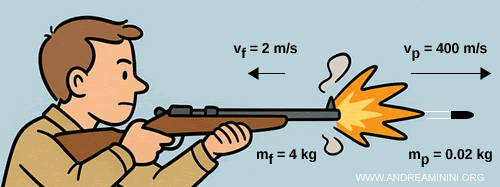
The bullet’s momentum is:

$$ p_p = m_p \cdot v_p = 0.02 \cdot 400 = 8 \,\text{kg·m/s} $$

By conservation of momentum, the rifle must acquire an equal and opposite momentum:

$$ p_f = -8 \,\text{kg·m/s} $$

This corresponds to a recoil velocity of 2 m/s:

$$ v_f = \frac{p_f}{m_f} = \frac{-8}{4} = -2 \,\text{m/s} $$

This is the origin of recoil in firearms.

Overall, the total momentum remains zero:

$$ p_{\text{tot}} = p_p + p_f = 8 - 8 = 0 $$

The distribution, however, is very uneven: the light bullet gains a large velocity, while the heavy rifle moves slowly in the opposite direction.

Theoretical Foundation

The conservation of momentum stems from a deeper principle: spatial symmetry.

Space is said to be homogeneous if the laws of physics are identical at every point.

In other words, shifting a system a few meters to the left or right does not alter the equations that govern its motion.

Noether’s theorem establishes that every continuous symmetry of a physical system corresponds to a conserved quantity:

• Time symmetry
  Invariance under time translations implies conservation of energy.
• Spatial symmetry
  Invariance under spatial translations implies conservation of momentum.
• Rotational symmetry
  Invariance under rotations implies conservation of angular momentum.

Thus, translational invariance guarantees that momentum is conserved.

And so on.