Lepton Numbers

Because there are three distinct families of leptons, physicists define three separate lepton numbers:

• Electron number $L_e$
• Muon number $L_\mu$
• Tau number $L_\tau$

For each family, ordinary leptons carry a value of $+1$, while their antiparticles carry $-1$.

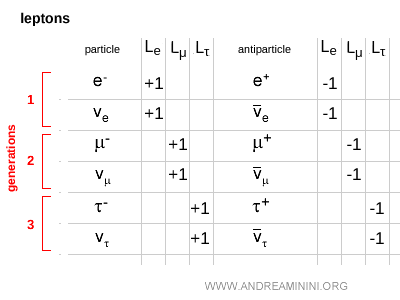
For example, in the first lepton family, the electron $ e^- $ and the electron neutrino $ \nu_e $ both have an electron lepton number $ L_e = +1 $, while their antiparticles - the positron $ e^+ $ and the electron antineutrino $ \bar{\nu}_e $ - carry $ L_e = -1 $. All their other lepton numbers are zero. 

Conservation of Lepton Number

Lepton numbers are conserved in every fundamental interaction.

In practice, this means that the total lepton number before a reaction must equal the total lepton number after it.

Any process that breaks this rule is forbidden in nature - at least within the framework of the Standard Model.

• Strong interaction
  The strong force doesn’t involve leptons at all, so lepton numbers stay unchanged. No leptons are ever created or destroyed in a purely strong interaction.
• Electromagnetic interaction
  The electromagnetic force acts on charged leptons (like electrons), but it never alters which family they belong to. As a result, lepton numbers remain the same.
• Weak interaction
  Weak interactions can convert one lepton into another within the same family. Even so, each family lepton number is conserved independently. Any process that would violate this rule simply cannot occur in nature.
  

  Note. The weak interaction conserves the lepton numbers of the three families separately. For instance, an electron or electron neutrino (first generation) cannot turn into a muon or tau (second or third generation), and vice versa. That’s why we speak of three independent lepton numbers ($ L_e,\quad L_\mu,\quad L_\tau $), each preserved in weak processes. This kind of separate conservation applies only to leptons. Quarks behave differently: weak interactions allow quarks from different generations to mix through the CKM matrix (Cabibbo - Kobayashi - Maskawa), which means there are no strictly conserved “quark numbers” analogous to $L_e$, $L_\mu$, or $L_\tau$.

Example

The negative muon $\mu^-$ belongs to the second lepton generation.

In a vacuum, it undergoes spontaneous weak decay into three particles: an electron ($ e^- $), an electron antineutrino ( $ \bar{\nu}_e $ ), and a muon neutrino ( $ \nu_\mu $ ).

$$ \mu^- \rightarrow e^- + \bar{\nu}_e + \nu_\mu $$

To check if this decay is allowed, we look at the lepton numbers of all the particles involved:

$$ \underset{L_\mu = +1}{\mu^-} \;\;\rightarrow\;\; \underset{L_e = +1}{e^-} \;+\; \underset{L_e = -1}{\bar{\nu}_e} \;+\; \underset{L_\mu = +1}{\nu_\mu} $$

Now let’s verify conservation for each lepton family number:

• Electron number ( $ L_e $ )
  Initially, the total electron number is zero: $$ L_e^{\text{initial}} = 0 $$ After the decay, we have: $$ L_e^{\text{final}} = +1 \ (\text{from } e^-) + (-1) \ (\text{from } \bar{\nu}_e) = 0 $$ So electron number is conserved. $$ L_e^{\text{initial}} = L_e^{\text{final}} = 0 $$
• Muon number ( $L_\mu$ )
  At the start: $$ L_\mu^{\text{initial}} = +1 \ (\text{from } \mu^-) $$ After the decay: $$ L_\mu^{\text{final}} = +1 \ (\text{from } \nu_\mu) $$ So the muon number is conserved. $$ L_\mu^{\text{initial}} = L_\mu^{\text{final}} = +1 $$
• Tau number ( $L_\tau $ )
  No tau leptons are involved, so the tau number is zero both before and after: $$ L_\tau^{\text{initial}} = L_\tau^{\text{final}} = 0 $$

This shows that muon decay respects the separate conservation of all three lepton numbers, which is why it occurs in nature.

Example 2

Now consider a different, purely hypothetical decay:

$$ \mu^- \rightarrow e^- + \gamma $$

Here are the non-zero lepton numbers of the particles involved:

$$ \underset{L_\mu = +1}{\mu^-} \;\;\rightarrow\;\; \underset{L_e = +1}{e^-} + \gamma $$

In this case, lepton number conservation is violated for both $L_e$ and $L_\mu$, since no neutrinos are produced to balance the change.

For that reason, this decay does not take place in nature - or, if it does, it is so extremely rare that it has never been observed.

Further Remarks

Some additional notes on lepton numbers:

• Neutrino oscillations and possible violations
  The discovery of neutrino oscillations showed that, over long distances, neutrinos can switch from one family type to another. This suggests a subtle violation of individual lepton number conservation, even though the total lepton number remains conserved: $$L = L_e + L_\mu + L_\tau$$ If confirmed, this would point toward new physics beyond the Standard Model.

And the discussion continues…