OZI Rule
The OZI rule states that a decay process is suppressed (i.e. rare) if its Feynman diagram can be split into two disconnected parts by cutting only gluon lines. Such decays are not forbidden, but they occur far less frequently than one would normally expect.
When the quarks inside the initial particle can simply rearrange to form the final products, the decay proceeds readily-even if that channel is not the most energetically favorable.
By contrast, if the original quarks must first annihilate completely into gluons, which then generate new quark-antiquark pairs, the process is far rarer (OZI suppression). This is because high-energy gluons couple only weakly, a consequence of QCD’s asymptotic freedom.
In short, a strong decay in which the constituent quarks directly recombine into new particles is far more likely than one requiring complete annihilation into gluons followed by the creation of new quark pairs.
This explains why Feynman diagrams that can be divided by cutting only gluon lines correspond to suppressed processes (the OZI rule).
Note. The rule is named after three theorists-Susumu Okubo, George Zweig, and Jugoro Iizuka. In the 1960s, while studying meson decay data, they noticed an anomaly: certain decay channels, though allowed by energy conservation and symmetry principles, occurred much less often than expected. To account for this, they formulated what is now known as the OZI rule. It explains why some decays that should be “strong” in theory are in practice highly suppressed: the outcome depends on whether the quarks can directly rearrange into the final states, or whether they must first annihilate into gluons.
A Practical Example
The $\phi$ meson consists of an $s\bar{s}$ pair and has a mass of about $1020 \,\text{MeV}/c^2$.
It decays mainly in two ways:
- Decay into two kaons
In the channels $\phi \to K^+K^-$ or $\phi \to K^0\bar{K}^0$, the $s\bar{s}$ pair inside the $\phi$ meson rearranges directly to form two kaons, without fully annihilating into gluons. $$ \phi \;\;\to\;\; K^+K^- \quad \text{or} \quad K^0\bar{K}^0 $$ Each kaon has a mass of roughly $495 \,\text{MeV}/c^2$, giving a combined final-state mass of about $990 \,\text{MeV}/c^2$. While this channel is not especially favored energetically, it is straightforward at the quark level: the $s\bar{s}$ pair in the $\phi$ combines with a $u\bar{u}$ pair created by a gluon, producing two kaons. This is the dominant decay observed experimentally.
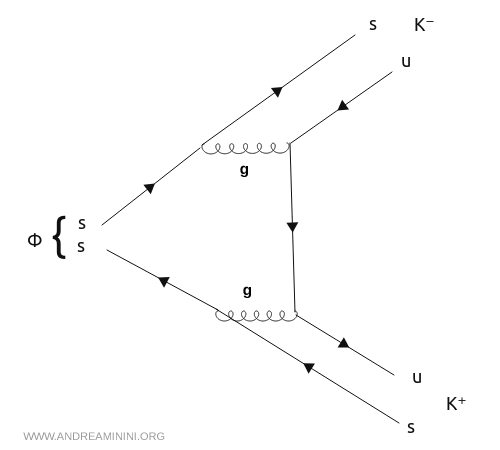
- Decay into three pions
The $\phi$ can also decay into three pions, $\pi^+\pi^-\pi^0$: $$ \phi \;\;\to\;\; \pi^+\pi^-\pi^0 $$ The three pions together have a mass of about $405 \,\text{MeV}/c^2$. From an energy perspective this channel is much more favorable than the two-kaon decay, since the final-state mass is lower. However, pions are built from $u$ and $d$ quarks, whereas the $\phi$ contains $s\bar{s}$. To produce them, the $s\bar{s}$ pair must first annihilate into gluons, which then generate $u\bar{u}$ and $d\bar{d}$ pairs. These pairs recombine to form three pions. Although energetically accessible, this mechanism is OZI-suppressed and thus extremely rare. In terms of Feynman diagrams, the process can indeed be split into two parts by cutting only gluon lines, as the OZI rule specifies.
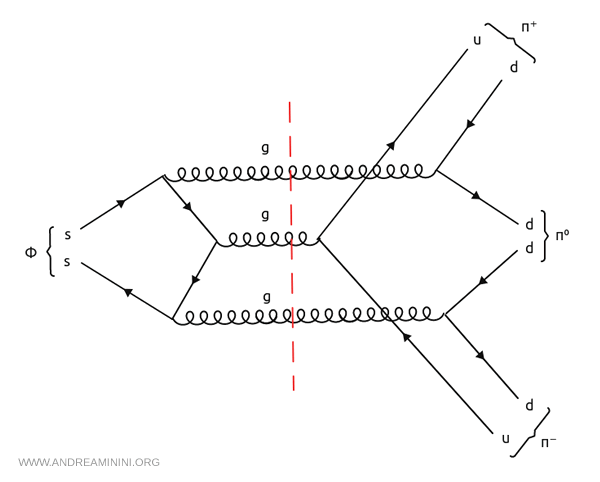
In conclusion, the $\phi$ meson decays predominantly into two kaons, even though the three-pion channel would be more favorable energetically.
The reason is simple: the two-kaon decay makes direct use of the original quarks, whereas the three-pion decay requires annihilation into gluons and the creation of entirely new quark pairs.
