Bisector Equation in the Cartesian Plane

The bisector of the Cartesian plane is a straight line passing through the origin, where points are equidistant from the coordinate axes. $$ |y| = |x| $$

The x-coordinate and y-coordinate of the bisector are equal in absolute value.

In the Cartesian plane, there are two bisectors:

• Bisector of the First and Third Quadrants
  The coordinates (x, y) of the bisector in the first and third quadrants have the same sign and equal absolute value. $$ y = x $$ This equation has infinitely many solutions, with every point on the bisector representing a solution.
  
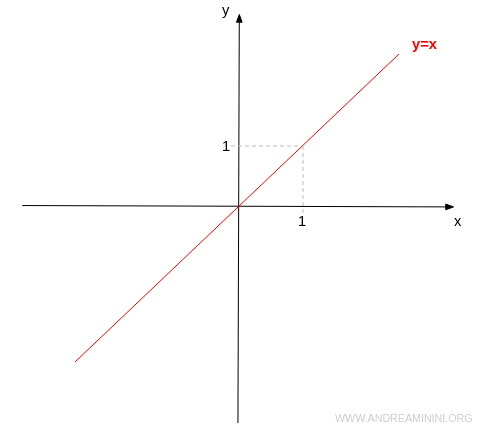
• Bisector of the Second and Fourth Quadrants
  The coordinates (x, y) of the bisector in the second and fourth quadrants have opposite signs but equal absolute value. $$ y = -x $$ Like the first case, this equation also has infinitely many solutions, and every point on the bisector is a valid solution.
  

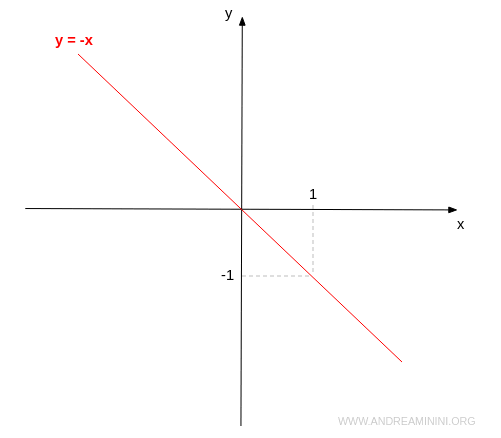
The two bisectors in the Cartesian plane are specific cases of linear equations.