Geometry Problem 2

In this right-angled triangle, the only known information is that the angle at vertex C is 52°, and the bisectors of the angles at vertices A and C are given. The task is to calculate the sum of angles x and y.

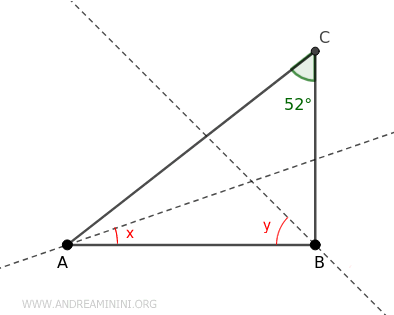
Since this is a right-angled triangle, it’s immediately apparent that the angle at vertex B is a right angle (90°), even though it’s not explicitly marked in the diagram.

$$ A \hat{B} C = 90° $$

Knowing that the bisector splits the angle $ A \hat{B} C $ in half, we can determine the measure of angle y by dividing the angle at vertex B by two.

$$ y = \frac{A \hat{B} C }{2} $$

$$ y = \frac{90°}{2} $$

$$ y = 45° $$

The sum of the interior angles of any triangle always equals 180°.

$$ B \hat{A} C + A \hat{B} C + A \hat{C} B = 180° $$

With two of the triangle’s angles already known, we can find the third angle by subtracting them from 180°.

$$ B \hat{A} C + 90° + 52° = 180° $$

$$ B \hat{A} C = 180° - 90° - 52° $$

$$ B \hat{A} C = 38° $$

Now that we know the angle $ B \hat{A} C $, we can also find angle x, as the bisector splits this angle in half as well.

$$ x = \frac{B \hat{A} C} {2} $$

$$ x = \frac{38°}{2} $$

$$ x = 19° $$

Thus, the values of angles x and y are x = 19° and y = 45°.

Their sum is:

$$ x + y = 19° + 45° $$

$$ x + y = 64° $$

In conclusion, the sum of the measures of angles x and y is 64°.

This completes the solution to the problem.