Point

In Euclidean geometry, a point is one of the fundamental entities, along with lines and planes.

It is considered a primitive concept because it is not defined in terms of other geometric concepts. As such, it doesn't have a formal definition in terms of other geometric entities.

Intuitively, a point is seen as an object that has no dimensions (length, width, height), no shape, and cannot be divided into smaller parts. In Euclid's "Elements," a point is defined as "that which has no parts."

Although it has no dimensions, graphically a point is represented as a small mark, like a tiny circle or dot, to indicate its position.

However, it's important not to confuse the symbol used to represent it (for example, a circle) with the point itself. The symbol has physical dimensions, while the point is dimensionless and an abstract geometric concept that cannot be perfectly represented physically. So, when I draw a point on a piece of paper, I am merely representing a small mark that approximates the idea of a point.

In geometry, a point is represented by a capital letter, such as \( A \), \( B \), or \( C \).

A point can be considered as an indication of a position in space.

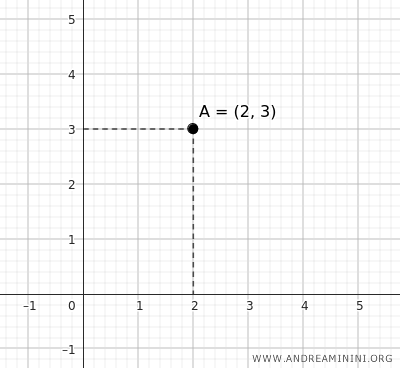
In a two-dimensional Cartesian plane, a point is described by a pair of coordinates \((x, y)\).

For example, point A at coordinates (2,3) in the Cartesian plane represents a precise position 2 units along the x-axis and 3 units along the y-axis.

In three-dimensional space, a point is described by a set of coordinates \((x, y, z)\).

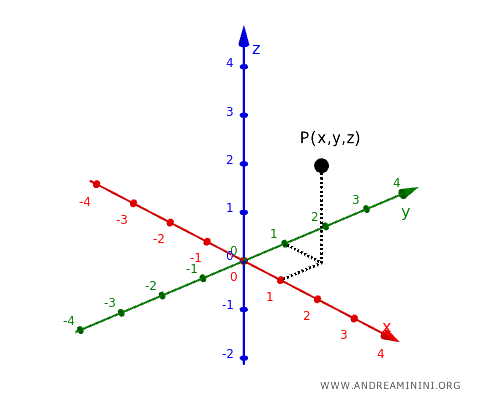
In Euclid's postulates, points are used to define other fundamental concepts:

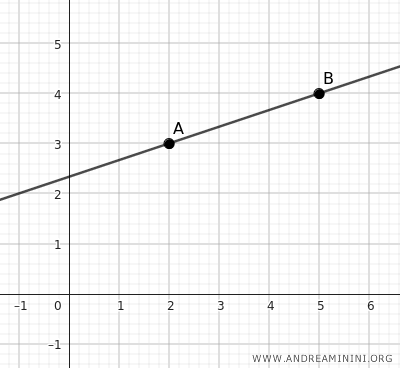
For example, a line is determined by two distinct points.

Any line can be thought of as an infinite collection of points aligned in the same direction.

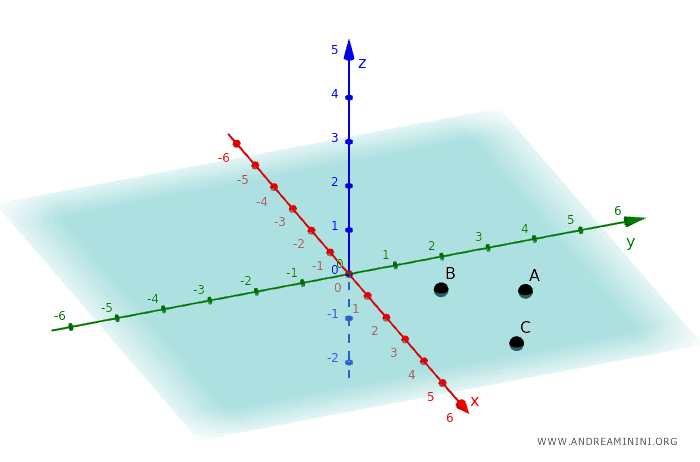
A plane is determined by three non-collinear points. It is a two-dimensional surface made up of infinite points extending infinitely.

In general, points are also used to construct more complex geometric figures, such as segments, angles, polygons, and curves.

And so on.