Weak Interaction

The weak interaction is one of the fundamental forces of nature, alongside the strong force, electromagnetism, and gravity. It acts on both leptons (such as electrons and neutrinos) and quarks, and operates through the exchange of mediator bosons: $W^+$, $W^-$, and $Z^0$. It is commonly known as the weak charge.

It is the only force that can change the flavor of elementary particles, turning one quark or lepton into another of the same family.

Because of this property, it is responsible for processes such as beta decay in unstable nuclei. And since neutrinos are produced and detected through weak interactions in their flavor states, this force is also indirectly tied to the phenomenon of neutrino oscillations.

Its range is extremely short (around $10^{-18}$ m), and its strength is far weaker than either the strong or electromagnetic forces. At low energies, it can be up to $10^{11}$ times weaker than electromagnetism.

It’s worth noting that the quoted values for the relative strengths of the forces are only rough orders of magnitude at low energies. In reality, the coupling constants vary with the energy scale of the process. Broadly speaking, the weak interaction is between about $10^{5}$ and $10^{13}$ times weaker than the strong force.

Note. Despite its weakness, the weak interaction plays an essential role in both particle physics and astrophysics - for instance, in the nuclear reactions that power stars.

Beta Decay and the Weak Interaction

The weak interaction underpins beta decay, a type of radioactive process that allows an unstable atomic nucleus to transform into a more stable one. 

A nucleus is unstable when it has an imbalanced neutron-to-proton ratio.

Beta decay helps restore balance by converting a neutron into a proton or vice versa. It is one of the main forms of natural radioactivity, along with alpha and gamma decay.

• Beta decay (β⁻)
  A neutron transforms into a proton, emitting an electron and an electron antineutrino: $$ n \;\;\to\;\; p + e^- + \bar{\nu}_e $$ On the quark level, a down quark becomes an up quark by emitting a virtual \$W^-\$ boson, which promptly decays into \$e^-\$ and \$\bar{\nu}\_e\$.
  
• Beta decay (β⁺)
  A proton transforms into a neutron, emitting a positron and an electron neutrino: $$p \;\;\to\;\; n + e^+ + \nu_e$$ Here, an up quark changes into a down quark by emitting a virtual \$W^+\$ boson, which decays into \$e^+\$ and \$\nu\_e\$.
  

  

This mechanism allows the nucleus to adjust its neutron-to-proton ratio, moving toward a more stable energy configuration.

Beyond being one of the natural sources of radioactivity, beta decay also plays a central role in the nuclear reactions that power stars - including those at the heart of the Sun.

Types of Weak Interactions (Neutral and Charged)

The weak force comes in two distinct forms.

• Neutral weak interactions (NC, Neutral Current)
  These are mediated by $ Z $ bosons. In such processes, the fermion that enters the vertex is the same one that comes out: there is no change of flavour, just as in electromagnetic or strong interactions. What sets them apart, however, is their violation of parity - a striking signature that makes them detectable even when they subtly “contaminate” processes otherwise governed by electromagnetism, such as in certain atomic physics experiments.

  Note. Charged weak interactions had already been identified in the 1930s, thanks to Fermi’s pioneering work on beta decay. Neutral weak interactions, by contrast, were only predicted later - in the late 1960s - by Glashow, Weinberg, and Salam within the framework of the electroweak theory (GWS). Their prediction was dramatically confirmed at CERN in 1973, marking a milestone in particle physics: until then, only $W$-mediated processes were known; the discovery of $Z$-mediated interactions was a breakthrough.

• Charged weak interactions (CC, Charged Current)
  These are mediated by $ W $ bosons. Unlike any other fundamental interaction, they can change the flavour of particles. For example, an up quark can turn into a down quark, or an electron into an electron neutrino. This ability to alter flavour makes charged weak interactions the true engine of decay processes, such as nuclear beta decay.

  Note. In the strong interaction, quarks may switch colour (e.g., from red to green) but not flavour; in electromagnetic interactions, fermions (quarks and leptons) can emit or absorb photons without changing either flavour or charge. The same is true for neutral weak interactions (NC), mediated by the $Z$ boson. By contrast, in charged weak interactions (CC), mediated by the $W^\pm$ bosons, a particle can change flavour: for instance, an up quark can become a down quark, enabling a proton to turn into a neutron, or vice versa.

Before diving into examples, here’s a table that highlights the key differences between neutral and charged weak interactions - a quick reference to keep the two straight at a glance.

Type of interaction	Mediator	Flavour change	Distinctive feature
Neutral weak (NC)	Z0 boson	No	Violates parity but preserves both charge and particle identity
Charged weak (CC)	W± bosons	Yes	Drives decay processes, turning one fermion into another

Practical Examples

Classic examples of weak interactions include neutrino - electron scattering $ \nu_{\mu} + e^- \to \nu_{\mu} + e^- $ and neutrino - proton scattering $ \nu_{\mu} + p \to \nu_{\mu} + p $.

Neutrino - electron scattering

In neutrino - electron scattering, a neutrino ($\nu$) collides with an electron ($e^-$), deflecting it and transferring part of its energy and momentum: $$ \nu + e^- \;\to\; \nu + e^- $$ This process is exceedingly rare, since neutrinos are electrically neutral and therefore do not interact electromagnetically. The weak force provides the only possible channel.

Two distinct mechanisms are possible:

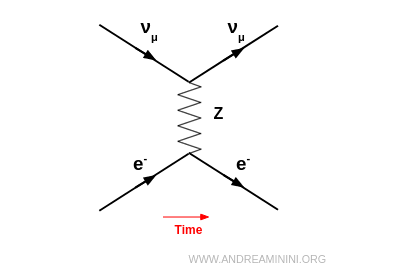
• Neutral-current scattering (mediated by $Z^0$)
  This occurs for all neutrino flavours ($\nu_e, \nu_\mu, \nu_\tau$). The neutrino exchanges a virtual $Z^0$ boson with the electron and emerges with the same flavour: $$ \nu_\mu + e^- \;\to\; \nu_\mu + e^- $$ Only the energy and direction change, making it an elastic collision.
  
• Charged-current scattering (mediated by $W^\pm$)
  In this case, an electron neutrino $\nu_e$ is converted into an electron by exchanging a $W$ boson with the target electron, which in turn becomes an electron neutrino: $$ \nu_e + e^- \;\to\; e^- + \nu_e $$ Effectively, the neutrino and the electron swap identities. The final state resembles that of neutral scattering, but the mediator is a $W$ rather than a $Z$ boson.

Note. Neutrino - electron scattering was among the first processes used to confirm the existence of neutral weak currents at CERN in 1973. It is regarded as a “clean” probe, since it does not involve nucleons or the strong force, allowing a direct test of the electroweak theory.

Neutrino - proton scattering

In neutrino - proton scattering, a neutrino interacts directly with a proton.

Because neutrinos carry no electric charge and are unaffected by the strong interaction, the only possible exchanges are through the weak bosons $W^\pm$ and $Z^0$.

As in the neutrino - electron case, there are two main categories:

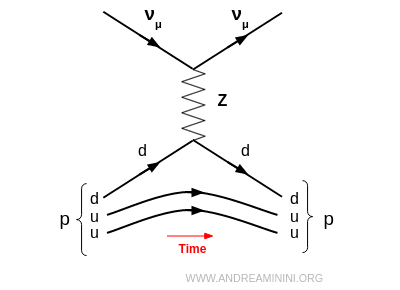
• Neutral-current scattering (NC)
  Mediated by the $Z^0$ boson. The neutrino retains its flavour, and the proton remains unchanged. Only their energy and momentum are redistributed (elastic scattering). For instance, a muon neutrino scattering off a proton: $$ \nu_\mu + p \;\to\; \nu_\mu + p $$ This reaction played a central role in the 1973 CERN discovery of neutral currents.
  
• Charged-current scattering (CC)
  Mediated by the $W^\pm$ boson. The neutrino converts into a charged lepton, while the proton is transformed into a different nucleon (proton ↔ neutron). For example, when an electron neutrino interacts with a proton, it produces a positron and converts the proton into a neutron: $$ \nu_e + p \;\to\; e^+ + n $$ This process is essentially the inverse of beta decay.

Both types of scattering are exceptionally rare. Observing them requires massive detectors and extremely intense neutrino beams.

Weak Interaction among Leptons

The charged weak interaction between leptons, mediated by the $W^\pm$ bosons, enables a neutrino (charge $0$) and its corresponding charged lepton (charge $-e$) to convert into one another, but only within the same generation.

The weak force acts universally on all leptons - electrons, muons, taus, and their associated neutrinos.

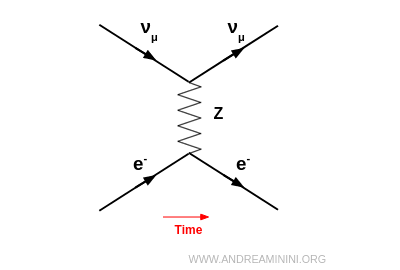
In a neutral-current scattering (mediated by $ Z^0 $), two leptons interact by exchanging a $Z^0$ boson.

Here, the particle identities remain unchanged (no flavour conversion), but their energy and momentum are redistributed.

For instance, a muon neutrino can scatter elastically off an electron via $Z^0$ exchange: $$ \nu_\mu + e^- \;\to\; \nu_\mu + e^- $$ Both the neutrino and the electron retain their identity, while only their energy and direction are altered.

In a charged-current scattering (mediated by $W$), a charged lepton and the neutrino of the same generation convert into one another (e.g. $ e^- \leftrightarrow \nu_e $, $ e^+ \leftrightarrow \bar{\nu}_e $) through $W$ exchange.

$$ l^- \leftrightarrow \nu_l + W^- $$

So, in weak interactions, leptons always transition within their own generation.

• The electron $(e^-)$ interacts only with its corresponding electron neutrino $(\nu_e)$
• The muon $(\mu^-)$ interacts only with the muon neutrino $(\nu_\mu)$
• The tau $(\tau^-)$ interacts only with the tau neutrino $(\nu_\tau)$

In every Feynman vertex, lepton number conservation is strictly maintained.

Explanation. In weak interactions, each charged lepton couples exclusively to its own generation neutrino via the $W$ boson. Consequently, at a weak vertex in a Feynman diagram, the electron number $L_e$, muon number $L_\mu$, and tau number $L_\tau$ are conserved independently. For example, $e^- \leftrightarrow \nu_e$ and $\mu^- \leftrightarrow \nu_\mu$. This means an electron can never convert into a muon neutrino, nor can a muon become an electron neutrino. Put simply, the weak force conserves lepton number separately within each family.

The interaction can be described equivalently as the emission or absorption of a $W$ boson.

Emission of a W boson

Any charged lepton can emit a $W$ boson:

• A negatively charged lepton ($e^-$, $\mu^-$, $\tau^-$) can convert into its neutrino by emitting a $W^-$: $$ \ell^- \;\to\; \nu_\ell + W^- $$
• A positively charged lepton ($e^+$, $\mu^+$, $\tau^+$) does the opposite, converting into its antineutrino while emitting a $W^+$: $$ \ell^+ \;\to\; \bar{\nu}_\ell + W^+ $$

Thus, negative leptons emit $W^-$, while their antiparticles emit $W^+$.

For example, a negative muon $\mu^-$ may transform into a muon neutrino $\nu_\mu$, emitting a $W^-$. That $W^-$ can then be absorbed by an electron neutrino $\nu_e$, producing an electron $e^-$: $$ \mu^- + \nu_e \;\to\; \nu_\mu + e^- $$

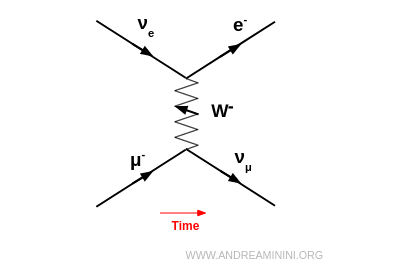
If the emitted $W^-$ is not absorbed, it may instead decay into an electron and an electron antineutrino: $$ W^- \;\to\; e^- + \bar{\nu}_e $$ In this case, the overall process is muon decay: $$ \mu^- \;\to\; \nu_\mu + e^- + \bar{\nu}_e $$

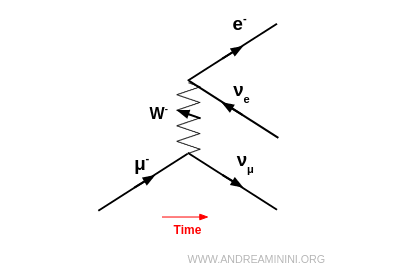
Absorption of a W boson

Conversely, leptons can absorb a $W$ boson, turning into their corresponding partners:

• A neutrino can absorb a $W^-$, becoming the corresponding negatively charged lepton: $$ \nu_\ell + W^- \;\to\; \ell^- $$
• An antineutrino can absorb a $W^+$, becoming the corresponding positively charged lepton: $$ \bar{\nu}_\ell + W^+ \;\to\; \ell^+ $$

For instance, a positron ($e^+$) can convert into its electron antineutrino $\bar{\nu}_e$ by emitting a $W^+$. That same $W^+$ may then be absorbed by a muon antineutrino $\bar{\nu}_\mu$, producing a positive muon $\mu^+$. The full process is: $$ e^+ + \bar{\nu}_\mu \;\to\; \bar{\nu}_e + \mu^+ $$

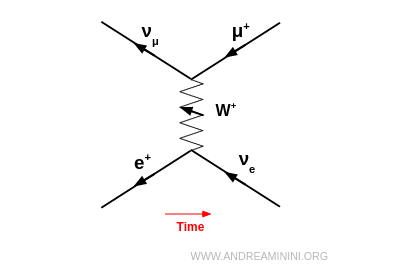
Because these are antiparticles, their arrows in the Feynman diagram are drawn opposite to the flow of time, though the diagram is still read left to right along the physical time axis.

Weak interaction among quarks

The charged weak interaction between quarks, mediated by $W^\pm$ bosons, allows a quark with charge $+\tfrac{2}{3}e$ to turn into one with charge $-\tfrac{1}{3}e$, or vice versa. These transitions can occur not only within the same generation but also across different ones, with probabilities determined by the elements of the CKM matrix.

For instance, quarks with charge $-\tfrac{1}{3}$ (down $d$, strange $s$, bottom $b$) can transform into quarks with charge $+\tfrac{2}{3}$ (up $u$, charm $c$, top $t$) by emitting a $W^-$ boson.

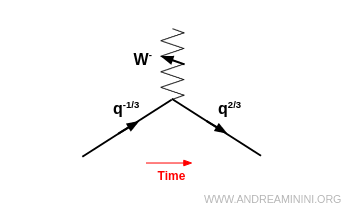
During this process, the quark preserves its baryon number but changes its flavour.

Note. The $ W^- $ boson does not “carry away” the flavour. It is the quark itself that switches flavour during the transition.

The emitted $W$ boson can:

• decay spontaneously into a lepton - antineutrino pair ($e^- + \bar\nu_e$, $\mu^- + \bar\nu_\mu$, etc.).
  

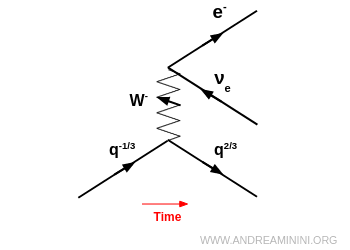
  Note. This is exactly what happens in beta decay $ β^- $, when a neutron decays into a proton: $ n \to p +e^- + \bar{\nu}_e $
  

• be absorbed by a neutrino, turning it into the corresponding charged lepton (e.g. $ \nu_e \to e^- $). This leads to a semileptonic process such as $ d + \nu_e \to u + e^- $.
  
• be absorbed by another quark, producing a flavour change at a different weak vertex (a purely hadronic process).

  For example, the $ \Lambda $ particle is a baryon made of three quarks (up, down, strange), belonging to the hyperon family. It decays into a proton and a pion, $ \Lambda \to p + \pi^- $, by converting a strange quark (s) into an up quark (u).
  
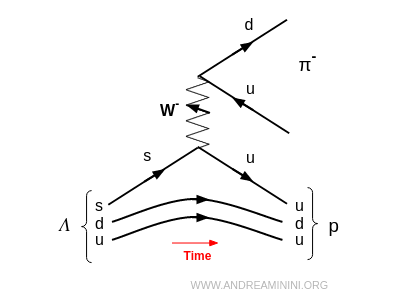
  This case illustrates a crucial point: a strange quark (s) transforms into an up quark (u), showing a transition between different quark generations.

Initially, physicists expected quarks, like leptons, to obey the rule that weak vertices are confined to a single generation. To their surprise, they discovered that quarks can change flavour across generations as well.

In 1963, Nicola Cabibbo proposed that down-type quarks ($d, s$) do not take part in weak interactions as “pure” states, but as linear combinations. He introduced the Cabibbo angle to explain decays involving strangeness change.

A decade later, in 1973, Makoto Kobayashi and Toshihide Maskawa extended this framework to three quark generations.

This led to the formulation of the CKM matrix (Cabibbo - Kobayashi - Maskawa), which describes how quark generations mix in weak interactions, with down-type states ($d,s,b$) appearing as linear combinations.

In practice, the down quark $ d $ does not couple exclusively to the $ u $ quark, but to a mixture of $d, s, b$. The same holds for $c$ and $t$.

$$ (u,d'),\quad (c,s'),\quad (t,b') $$

Here $d', s', b'$ are “mixed quarks,” i.e. linear combinations of $d, s, b$.

$$ d' = V_{ud}\, d + V_{us}\, s + V_{ub}\, b $$

$$ s' = V_{cd}\, d + V_{cs}\, s + V_{cb}\, b $$

$$ b' = V_{td}\, d + V_{ts}\, s + V_{tb}\, b $$

For example, $V_{ud}$ tells us how much the $d$ quark contributes to $d'$, $V_{us}$ how much the $s$ quark contributes, and so on.

In compact form, these linear combinations can be written as a vector - matrix product: 

$$
\begin{pmatrix} d' \\ s' \\ b' \end{pmatrix}
=
\begin{pmatrix}
V_{ud} & V_{us} & V_{ub} \\
V_{cd} & V_{cs} & V_{cb} \\
V_{td} & V_{ts} & V_{tb}
\end{pmatrix}
\begin{pmatrix} d \\ s \\ b \end{pmatrix}
$$

This coefficient matrix $V_{ij}$ is what we call the CKM matrix (Cabibbo - Kobayashi - Maskawa).

If it were exactly the identity matrix, we would simply have $d'=d$, $s'=s$, $b'=b$.

But it isn’t: although the CKM matrix looks close to the identity, it is not identical.

This means quarks can change flavour not only within the same generation but also across generations when they interact through the weak force.

Note. Without this mechanism, the $u$ quark could only convert into a $d$ and vice versa. Because $V_{us} \neq 0$, however, it can also convert into a strange $s$. This accounts for processes that change strangeness.

In short, the CKM matrix explains how up-type quarks ($u, c, t$) can turn into down-type quarks ($d, s, b$) with specific probabilities.

The experimentally determined CKM matrix (as of 2020) shows the size of these probability amplitudes:

$$ \begin{bmatrix} |V_{ud}| & |V_{us}| & |V_{ub}| \\ |V_{cd}| & |V_{cs}| & |V_{cb}| \\ |V_{td}| & |V_{ts}| & |V_{tb}| \end{bmatrix} = \begin{bmatrix} 0.97370 \pm 0.00014 & 0.2245 \pm 0.0008 & 0.00382 \pm 0.00024 \\ 0.221 \pm 0.004 & 0.987 \pm 0.011 & 0.0410 \pm 0.0014 \\ 0.0080 \pm 0.0003 & 0.0388 \pm 0.0011 & 1.013 \pm 0.030 \end{bmatrix} $$

From the first row, for example, we see that the up quark ($ u $) couples to a down quark ($ d $) with an amplitude of about 97%, to a strange quark ($s $) with about 22%, and to a bottom quark ($ b $) with only about 0.4%.

Note. The sum $97% + 22% + 0.4% $ exceeds 100% because these are amplitudes, not probabilities. The actual probabilities are obtained by squaring each coefficient: $$ |V_{ud}|^2 + |V_{us}|^2 + |V_{ub}|^2 = 1 $$ For the example above: $$ |V_{ud}|^2 \approx (0.974)^2 \approx 0.949 $$ $$  |V_{us}|^2 \approx (0.225)^2 \approx 0.051 $$ $$  |V_{ub}|^2 \approx (0.0038)^2 \approx 0.000014 $$ The sum then comes out exactly to 100%: $$ 0.949 + 0.051 + 0.000014 \approx 1.000. $$

These values tell us which weak decays are common and which are suppressed:

• $u \to d$ is the most likely transition, which is why protons and neutrons dominate ordinary matter.
• $s \to u$ is possible but less frequent, and underlies strange decays ($\Lambda, \Sigma, \Omega$).
• $t \to b$ is essentially guaranteed: the top quark almost always decays into a bottom quark.

Thus, a $u$ quark can emit a $W^+$ and become a $d$, but also - less frequently - an $s$ or a $b$.

Note. For leptons, the weak vertex always connects particles within the same generation, preserving lepton numbers. Mixing across generations appears only later, through neutrino oscillations. For quarks, by contrast, inter-generational mixing is built directly into the charged weak vertex and is described by the CKM matrix. The principle is the same - the $W$ boson mediates transitions between “up” and “down” partners - but the pairing is no longer strictly confined to a single generation: the weak force enables mixed transitions between quark states from different generations.

Notes

Additional remarks on weak interactions:

• Neutral weak contributions within electromagnetic processes
  In any photon-mediated scattering (electromagnetic interaction), there is in principle also a corresponding diagram mediated by the $Z^0$ boson (neutral weak interaction). At low energies, however, the $Z$ amplitude is negligible compared with photon exchange and can be safely ignored. Only at very high energies - comparable to the $Z^0$ boson mass (about $91$ GeV) - does the $Z$ contribution become significant and measurable.
  

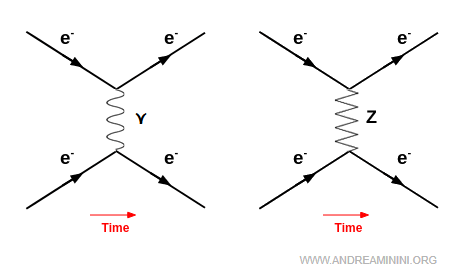
  Note. A landmark example comes from high-energy electron - positron scattering ($e^- + e^+ \to \mu^- + \mu^+$) studied at DESY (Deutsches Elektronen-Synchrotron) in Hamburg during the 1970s and 1980s, where corrections from neutral boson exchange were observed. This provided experimental evidence of weak effects even in electromagnetic processes: effectively, a tiny correction to Coulomb’s law, vanishing at low energies. To isolate a pure neutral current free of electromagnetic overlap, the cleanest probe is neutrino scattering, since neutrinos carry no charge and thus do not couple to photons. Such experiments, however, are notoriously challenging due to the extremely small neutrino cross-section.

 And so on.