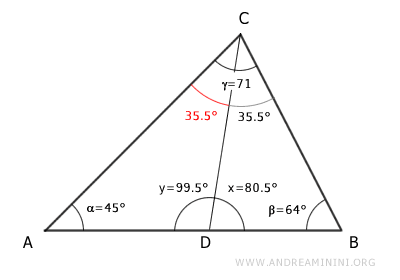
Geometry Problem 1

We have a triangle ABC where the angle at vertex A is 45°, and the angle at vertex B is 64°. Segment CD is the bisector of the angle at vertex C. Find the measures of angles x and y.
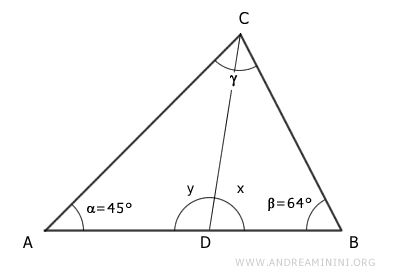
the triangle

Solution

In any triangle, the sum of the interior angles is always 180°.

$$ \alpha + \beta + \gamma = 180° $$

Given two angles, α = 45° and β = 64°, we can find the third angle by subtracting their sum from 180°.

$$ \gamma = 180° - \alpha - \beta $$

$$ \gamma = 180° - 45° - 64° $$

$$ \gamma = 71° $$

With the third angle, γ = 71°, now determined, we can move on to calculating angles x and y.

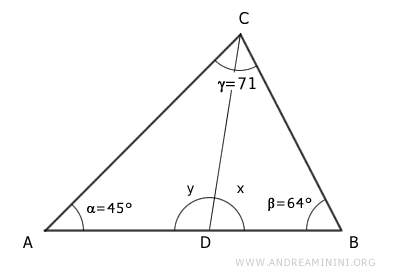
angle γ=71°

By definition, the angle bisector CD divides γ into two equal parts.

$$ \frac{γ}{2} = \frac{71°}{2} = 35.5° $$

From the diagram, it’s clear that the bisector splits triangle ABC into two smaller triangles, ACD and BCD.

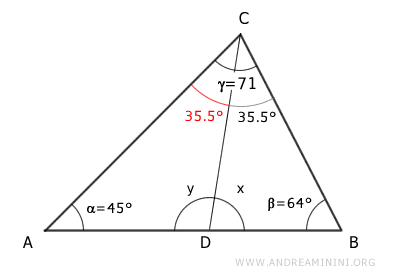
the bisector dividing angle gamma into two equal parts

In triangle ACD, we already know two angles: 35.5° and 45°, leaving y as the unknown angle.

Since the sum of the interior angles in any triangle is 180°, we can find y by subtracting the known angles from 180°.

$$ y + 45° + 35.5° = 180° $$

$$ y = 180° - 45° - 35.5° $$

$$ y = 99.5° $$

Thus, the measure of angle y = 99.5° has been found.

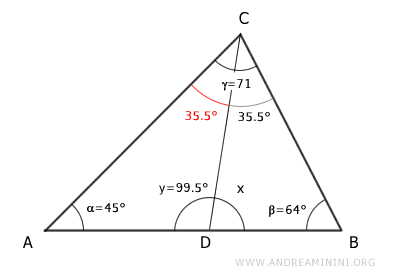
measure of angle y

Angles x and y are supplementary, meaning their sum is 180°.

$$ x + y = 180° $$

Since we already know that y = 99.5°, we can calculate x by subtracting y from 180°.

$$ x + 99.5 = 180° $$

$$ x = 180° - 99.5 $$

$$ x = 80.5° $$

Therefore, the angles are x = 80.5° and y = 99.5°.

solution to the problem

And with that, the problem is solved.